This definition embodies four concepts:
- Codification - Rigorous, storable, independent description. The result of agreements.
- Constraints - Conditions that define the implementation(s). They must exist before any comparison or communications exists.. The constraints create commonality.
- Comparison - Estimation of the similarities and differences as supported by the implementations and required by the use (application).
- Society - The economic or political grouping(s) that agrees to the constraints and utilizes the application.
Comparisons are a basic element of any communications Two or more common implementations (e.g. two balance scales), which may be physically independent or may use a single physical implementation at different times, are necessary for a comparison. The common aspects of such implementations may be defined by technical standards. Based on a need, a society produces and distributes (communicates) the technical standard(s) that defines the common implementations. So in a fundamental way, standards require communications and communications require standards. Thus, a step towards understanding standards is to understand communications. Information Theory offers a basic means to understand communications.
Applying Information Theory to Technical Standards
C. Shannon [3] defines information as the probability of a time series of symbols (e.g., bits) using the term "entropy." His Second Theorem defines the highest potential information state as the state with maximum entropy and no redundancy, that is, where the probability of each symbol received is uniform and independent of the previous symbols received. The highest potential information state, maximum entropy, has no redundancy, just ever changing, completely random symbols Ð white noise. Conversely, the lowest potential information state, zero entropy, has complete redundancy, the symbol stream is unchanging and there is no useful data. Useful information across a defined channel only exists in the range between zero and maximum entropy where there is some but not complete redundancy. Shannon offers a model of a communications system (Figure 1) that also can be related to technical standards.
The transmitter, channel and receiver exhibit a high level of commonality because the transmitter and receiver each operate over a common bandwidth with a common carrier frequency, related power levels, etc. The channel, too, is described by similar parameters. This, of course, is not surprising as the relationship between the three is likely to be defined by technical standards. The point is, for reliable communications to occur, not only must redundancy exist in the information transferred, commonality must also exist in the implementations and in the application. All communications requires two or more common implementations, the interconnecting channel and redundancy. Information Theory describes how redundancy is necessary to counteract the effects of noise. This paper proposes that redundancy is part of a broader concept termed commonality that is required for the transfer of information Ð communications.
Modifying Figure 1 and allowing bi-directional communications results in Figure 2. The system of constraints plus redundancy, now termed commonality, includes the elements bounded by the block of dotted lines in Figure 2. The commonality of two implementations at each end of a channel is created by the technical standards that define them. Additional commonality may also apply to both of the applications (use). The examples 4, 5 and 6 provided in the Appendix identify some relationships between applications and communications systems.
Noise may occur not only in the channel as defined in Information Theory but in every aspect of the model. As example, an effect similar to noise, distortion, results from imperfect implementations. For this reason the broader term Undesired Possibilities is used, which may impact all aspects of the communications system model except the end use or application.
Figure 2 encompasses both communications as developed by Information Theory and the more general technical standards model. Ten examples in the Appendix demonstrate how different technical standards apply to this model. Applying Information Theory to technical standards results in a more rigorous definition of the system of constraints than is developed in Information Theory and the definition of three new constructs: undefined channel, undesired possibilities and commonality.
When information is transferred across a defined channel, it is possible to calculate the source entropy in reference to zero entropy. On a defined channel, zero entropy is an identifiable state which may occur (e.g., when the channel fails in a steady state condition). But zero entropy is less likely on an undefined channel where multiple information or noise sources may exist. On an undefined channel when the extraneous input is avoided by identifying desired commonality (in effect, creating the channel), the unique information, redundancy and in-channel noise remain.
Another form of noise, often termed distortion, may be introduced by undesired differences between the common implementations. Calibration processes, which utilize a different communications channel, is one means to remove noise associated with differences between the common implementations (distortion). The term "undesired possibilities" combines noise (as defined in information theory) and distortion with the perturbations that appear over an undefined channel.
When symbol coding (an Information Theory term) or compression is employed, a specific commonality is implemented to reduce in-channel redundancy and make possible the transmission of increased unique information. A prior information transfer moved the compression to the common implementations for use. Looked at this way, in-channel redundancy is not reduced by compression, it is reduced by adding commonality to the implementations.
Channel coding (an Information Theory term), is part of the system of constraints that match the transmitter, receiver and channel. More complex channel coding can increase the communications rate of the channel up to the maximum rate possible (defined by the maximum entropy of the channel). Conversely when the transmitter, receiver, or channel are not well matched or defined, the effect (distortion) reduces the possible communications rate of the channel.
The single term commonality identifies the common relationship between the two sets of terms: distortion and channel coding, compression and redundancy. Together these four parameters may be optimized to maximize the performance of a communications system. Additionally commonality functions to identify, on undefined channels, a possible channel.
Economic processes often extract the commonalties to identify unique information. A buyer receiving two quotations from different suppliers for the same product or service evaluates the differences by removing the commonality between the two quotations. What is left identifies the information useful to the buyer. Even a zero difference (which is not the same as zero entropy) between the quotations is useful information to the prospective buyer. Note that the buyer example is similar to the operation of weighing two diamonds on a balance scale (Appendix example 4 ). The unique information (difference in weight [value] of the diamonds) is what is left after the Commonality is removed. These are examples of information transmitted over undefined channels.
The buyer and scale examples in the previous paragraph point out that it is useful on undefined channels to measure the source entropy (unique information) by subtracting the commonality from the maximum entropy. (The source entropy on any channel is not changed whether measured from maximum entropy or from zero entropy.)
Each of the three information transfers, codification, implementation and use, may occur over defined or undefined channels. Figure 3 includes both defined and undefined channel operation. The undesired possibilities as shown are within the maximum entropy. Undesired possibilities also exist in each box in the Figure.
The distribution of the common implementations shown in the center box of Figure 3 is also a form of information transfer . The solid arrows to designate the range of entropy would appear within the box but are not shown for simplicity. Notice that a small portion of the common implementation box in shown as source entropy, the remainder is commonality. Since common implementations are never identical, they also include some unique information (source entropy), which will appear as undesired possibilities in the next information transfer.
Figure 3 shows that communications itself is an evolutionary process built on successive transfers of more rigorous (sequentially better defined) information. The unique information (source entropy) is not usable information for communications. The unique information requires commonality to be useable.
Consider the user of a library of books and periodicals which is cataloged and organized. The user has learned over time the library's many different technical standards (alphabet, dictionary, date order, cataloging, indexes, search programs, shelves, building floors, etc.) which increase the commonality of the library. The maximum entropy of the library is limited largely by the overall physical size of the library; the "communications channel" to the user is undefined. If each page of each book and periodical was torn out and cut into individual letters (but not mixed), the pile created is much smaller than the original organized information, so much more unique information could be contained in the same size library building.
In this example, the commonality provided by the standards is removed and the source entropy and maximum entropy remain the same as before. Unfortunately the information that could be communicated has become useless. The trained library user is quite happy to have a library with less than the highest potential source entropy as it makes it possible to find the very small piece (relative to the total library) of useful information desired. This library example represents a case where the technical standards (commonality) that support access to unique information provide a very acceptable reduction in the potential source entropy. And without the effect of the technical standards, the source entropy appears no different than noise.
Each technical standard provides greater compression by creating a new symbol identifying the technical standard. Each standard succession provides yet greater compression using a set of symbols based upon, but independent of, the earlier successions. Compression, as discussed, only provides a conversion from redundancy to previously transferred commonality. Adding symbols has a more powerful effect by increasing the channel capacity exponentially (maximum entropy = log of the number of symbols) but only increasing the commonality linearly. Since the maximum entropy possible over undefined channels may be very high, increasing the number of symbols can increase the possible source entropy dramatically. Sets of symbols also provide a form of commonality that provides error control. Looked at very broadly, this exponentially increasing source entropy capacity coupled with linear increases in error rate and commonality, provides the mechanism that supports the expanding complexity seen in a technological society.
When the phrase, "200 horsepower V8" is communicated, three technical standard successions are used. The three successions are representational (number system), unit (horsepower) and similarity (V8). The use of these technical standards is predicated upon previously transferred commonality (i.e., the reader's understanding of each term in this phrase). Note how the communications efficiency increases as the succession of the technical standards increases. The representational standard offering 999 possible states provides little compression of the number 200. However horsepower is defined in more basic terms (length, weight and time) and provides more information than is contained in 10 letters. And the two characters V8, describe an eight cylinder, V shaped, four cylinders per side, four cycle, overhead valve, internal combustion engine; far more information than exists in (26+10)2 possible states.
Standards are symbols which naturally converge into groupings (based on the level of technology development) that provide significant communications efficiency and reliability advantages. The proposed taxonomy of standards also shows some correlation to DNA coding and to economic and technical history.
L. Gatlin [8] has proposed that the efficiency gained by the transition from individual DNA symbol encoding (A, T, C, G, representational standards) to encoding of groups of DNA symbols (condons [3 symbol] or gene [multi-condon], both similarity standards) underlies the rise of the vertebrates animal class. Understanding of the relationships between amino acids (defined by condons) and between proteins (defined by genes) is being developed. Such relationships might be considered compatibilities.
Looking at economic history, we have previously proposed that the emergence of similarity standards underlies the industrial revolution and that the emergence of compatibility standards provided the increased communications necessary for the information age [9].
The taxonomy of standards is a new way to comprehend how technical standards increase the communications efficiency of a specific system. Technical standards have sometimes been viewed as reducing the versatility and efficiency of a system, possibly as a result of misunderstanding the Information Theory term "redundancy." In fact, each new succession of technical standards functions to exponentially increase the maximum entropy (unique information) possible. Understanding standards as necessary for communications, not redundant or unnecessary, offers a clearer view of the importance of technical standards.
Comparing communications to entropy points out the differences. Communications is the result of a series of entropy transfers including both common and unique information. Figure 3 shows that successively more detailed common information is able to be transferred.
As was defined previously: a technical standard codifies for a society the constraints used for one or more comparisons between implementations. The constraints establish an entropy range between zero and the maximum entropy that is used for the communications associated with a desired application.
By expanding on the previous definition of a technical standard based upon the relationship established between Information Theory and technical standards, we can offer a more rigorous definition of a technical standard:
Linking communications to a continuum of entropy transfers offers a way of viewing communications of all kinds. In the case of serial communications over a defined channel, the use of technical standards (e.g., protocols) increases the transferred commonality per period and decreases the source entropy possible per period. To support the maximum useful information per period of transmission, a balance is necessary between the decrease in source entropy and the increase in redundancy due to the use of technical standards.
In addition, increasing commonality of the implementations can increase the defined communications channel capacity by compressing redundancy with source coding or increasing the channel capacity with improved channel coding. Greater commonality is dependent on the standards used and the implementation complexity. Thus, within the bounds of the maximum possible entropy of a defined channel, operating channel capacity is implementation and application dependent - related to the time and energy required to improve the implementations and the technical standards that define them.
Communication is achieved through a series of information transfers. Establishing commonality is the first phase of communication, that is, it is the first of one or more information transfers, over both defined and undefined channels. Standards are a part of the commonality required for communications. Standards support commonality not only for the first phase of communications, but also in all succeeding phases. The taxonomy of the succession of standards shows how increasingly complex commonalities can be used in communications, over both defined and undefined channels.
This paper has shown how technical standards are necessary to convert information to communications. Clearly there is much more work to be done to better understand the mathematical basis of technical standards. Next it is necessary to more rigorously develop the theories proposed and to further test these theories in actual practice. But the relationship of Shannon's "system of constraints" to technical standards is too strong to ignore. There is a mathematical basis of technical standards.
The authors wish to thank Frank Barnes and David Forney for their very helpful reviews and comments on this paper.
VOICE: +1 650 856-8836
Return to the directory of Ken's lectures, published articles and book reviews
[2] Useful definitions of these terms may be found in the Handbook of Automation Computation and Control Vol. 1, Edited By E. M. Grabbe, S. Ramo, D. Wooldridge, 1958, John Wiley and Son, Chapter 16 Information Theory by Peter Elias pages 16-01 to 16-48. Return to text
[3] C. Shannon, The Mathematical Theory of Communications, University of Illinois Press, 1963. Return to text
[4] K. Krechmer, The Fundamental Nature of Standards: Technical Perspective, IEEE Communications Magazine, June, 2000, page 70.Return to text
[5] Earlier papers by K. Krechmer and E. Baskin use the term stratum rather than succession. Return to text
[6] K. Krechmer, ibid. Return to text
[7] Discovery protocols include IETF Service Location Protocol, and the appropriate parts of Jini, Bluetooth, Universal Plug and Play and Home Audio Video Interoperability. R. Pascoe, Building Networks on the Fly, IEEE Spectrum, March, 2001. Return to text
[8] L. Gatlin, Information Theory and the Living System, Columbia University Press, 1972. Return to text
[9] K. Krechmer, ibid. Return to text
[10] In this case the codification is the mechanical arrangements (jigs and fixtures) used to guide the file that cuts the gear teeth. Return to text
[11] K. Krechmer, Technical Perspective. Return to text
(c) Copyright 1999. Communications Standards Review.
This page was last updated October 25, 2001.![]()

Figure 1. Information Theory model of a communications system.
The information source transmits the source entropy or unique information. across the system of constraints to the destination. The transmitter, channel (link between the transmitter, receiver and noise source) and receiver are a system of constraints (shown in dashed box in Figure 1). The system of constraints, if it meets the definition of technical standards (above), is a technical standard(s). The information source and destination together represent the communications application or use. 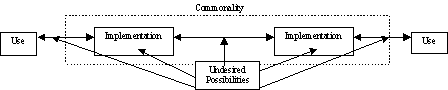
Figure 2. Expanded model of a communications system.
Any communications exist in a continuum. The earliest human communication is based on only simple assumptions. Next, some assumptions develop into conventions. Later, technical standards (codification) support more accurate communications than earlier conventions (understood, not codified) or even earlier assumptions (taken for granted, not understood). The earliest human communications does not pass via the defined channels described in Information Theory. We consider such communications to take place over undefined channels, which are described below.System of Constraints
The aspects of the transmitter, receiver and channel associated with communications form a system of constraints as noted by Shannon. When the system of constraints is defined, the transmitter is matched to the channel and the receiver in some agreed manner. Or the system of constraints may be undefined in which case there is no prior agreement between transmitter, channel and receiver, and whatever communications is possible is based on assumptions. Necessarily, the earliest technical standards (Examples 1, 3 and 4 in the Appendix) are transferred based on assumptions over undefined channels. When the system of constraints is previously agreed and defined, we consider it a defined channel exactly as defined in Information Theory.Undefined Channels
Communications over an undefined channel occurs in two phases. First the desired information source is identified from all sources possible by recognizing commonality (which may be based on previously transferred technical standards or assumptions) and separating out the undesired possibilities. Second, the in-channel noise is removed from the desired source by using redundancy. One example of this two phase process is the human ability to first identify, by recognizing a familiar voice or face (finding commonality), and then listen to, a specific conversation across a noisy room which may require the listener to use the redundancy of the human language to understand what is being said. Undesired Possibilities
The introduction of noise into a defined channel is well understood. An example of noise in an undefined channel may be seen when a library patron looks for a specific book. All other books are undesired possibilities, an expanded concept of noise, that may be removed using the organization of the library (often provided by technical standards). Undesired possibilities, including noise, are the limiting factor on undefined channels as well as on defined channels. Commonality
Shannon explains that redundancy is needed to extract the unique information in the presence of noise and that the redundancy represents the maximum compression possible, using symbol coding, without removing unique information. Redundancy includes all the constraints transferred over the channel. Compression may be employed to "remove" redundancy. However, compression is the result of a prior agreement, possibly a technical standard, applied to the transmitter and the receiver of a communications system. So the technical standard for compression is actually a replacement for redundancy. Another way to examine the same issue is to note that a defined channel without noise would require no redundancy for reliable communications but that "no noise" is a constraint which could be considered a prior agreement or even a technical standard.
Integrating technical standards with Information Theory demonstrates that a succession of increasingly complex technical standards provides the means to discern unique information from the clutter of undesired possibilities and information over an undefined channel. Figure 3 places the three representations of technical standards - codification, implementation and use - in relation to the entropy scale and demonstrates a continuum of communications. ![]()
![]()
![]()
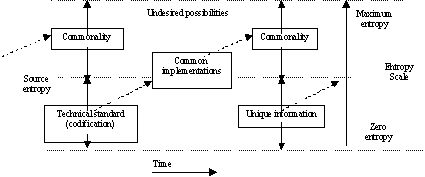
Figure 3. Communications Continuum
The solid arrows in Figure 3 identify ranges of entropy. The dotted arrows show that commonality is transferred from previous information transfers. The technical standard is usually codified via an undefined channel. Then the codified technical standard is used to create two or more implementations which have commonalties (likely transferred over an undefined channel). The implementations are used to transfer or communicate the source information (use) which may be over a defined channel. Then, it is quite possible that additional information transfers will continue.
Previous papers [4] by the authors have developed a taxonomy of standards using five successions [5] of technical standards (Table 1). Each succession is capable of supporting an unlimited number of technical standards, each of which may be considered a mathematical symbol. Classifying standards successions is similar to the classification of language into letter, word, phrase, sentence, and paragraph. Each succession is built on the previous layer, but is independently expandable. The term "succession" indicates that standards are not simply divisible into five distinct strata, but rather evolve from one layer to the next.
Standards succession Function
Representational Quantify relationships
Units Measurement of physical quantities
Similarity Define assemblies
Compatibility Relationship between assemblies
Adaptability Select compatibility standards or variables Table 1. The Succession of Standards
The first two successions of standards define common terms and physical units. The information flow of the first two successions of standards usually occurs over undefined channels. The third succession, similarity standards, is used to codify similar assemblies or constructions which also usually occurs over undefined channels. As example, similarity standards (Appendix, example 7) define the aspects of the nut and the bolt that result in their interworking. When there is an interrelationship between different similarity standards which supports communications, compatibility (the fourth succession) is created which is bound by the similarity standards employed. Compatibility standards create the defined channels where communications occurs. The EIA 232 interface (Appendix, example 8) is an example of a compatibility standard. Adaptability standards support negotiation over defined channels.
Information Theory describes a specific communications system, that of communicating across a defined channel. Adding the concepts of undefined channels, undesired possibilities, and commonality help explain communications as they occur in real life, not only over defined channels, but also over undefined channels. Undefined channels are those channels where there exists no prior agreements between the transmitter, channel and/or receiver, such that the receiver does not necessarily even expect to receive a communication. Undesired possibilities exist as all of the possible communications which could exist in an undefined channel. Undesired possibilities appear as noise and distortion in defined channels. Commonality identifies a common relationship within the information flow or the implementations and procedures used to support the information flow. On an undefined channels, commonality allows the identification of a possible channel. Often the commonality is defined by one or more technical standards.
Examples to help understand technical standards and the theories proposed
Communications Standards Revew
757 Greer Road
Palo Alto, California 94303-3024 USA
e-mail: krechmer@csrstds.comFootnotes
[1] David, Paul A., Some new standards for the economics of standardization in the information age, Economic Policy and Technology Performance, P. Dasgupta and P. Stoneman editors, Cambridge University Press, 1987. This model is a precursor of the taxonomy proposed.